Regression Discontinuity Designs

Adam Sales

2024-09-20

Data and Design

data(lsoSynth)

The data for this example were randomly simulated using the synthpop package in R based on data originally collected by Lindo, Sanders, and Oreopoulos (2010; hereafter LSO). (The original real data can be found here; code to simulate the fake data can be found here.)

At a major public university, students with a cumulative grade point average (GPA) below a pre-specified cutoff are placed on academic probation (AP). Students on AP are given extra support, and threatened with suspension if their GPAs do not improve. See LSO for details. Along with LSO, we will consider only students at the end of their first year at the university. The university consisted of three campuses, and they AP cutoff varied by campus. To simplify matters, we centered each student’s first year GPA on their campus’s cutoff, creating a new variable $R_i\equiv GPA_i -c_{campus[i]}$, where $GPA_i$ is student $i$’s first-year GPA, and $c_{campus[i]}$ is the AP cutoff for student $i$’s campus. A student $i$ is placed on AP if $R_i<0$ and avoids AP if $R_i\ge 0$.

We will attempt to estimate the average effect of AP placement on nextGPA, students’ subsequent GPA (either over the summer or in the following academic semester). This figure plots each the average nextGPA for students with distinct R values (i.e. centered first-year GPA). The cutoff for AP, 0, is denoted with a dotted line. The the sizes of the points are proportional to the natural log of the numbers of students with each unique value of R.

figDat <- aggregate(lsoSynth[,c('nextGPA','lhsgrade_pct')],by=list(R=lsoSynth$R),
                    FUN=mean,na.rm=TRUE)
figDat$n <- as.vector(table(lsoSynth$R))

with(figDat,
     plot(R,nextGPA,cex=log(n+1)/3,main='Average Subsequent GPA\n as a function of 1st-Year GPA,\n Centered at AP Cutoff'))
abline(v=0,lty=2)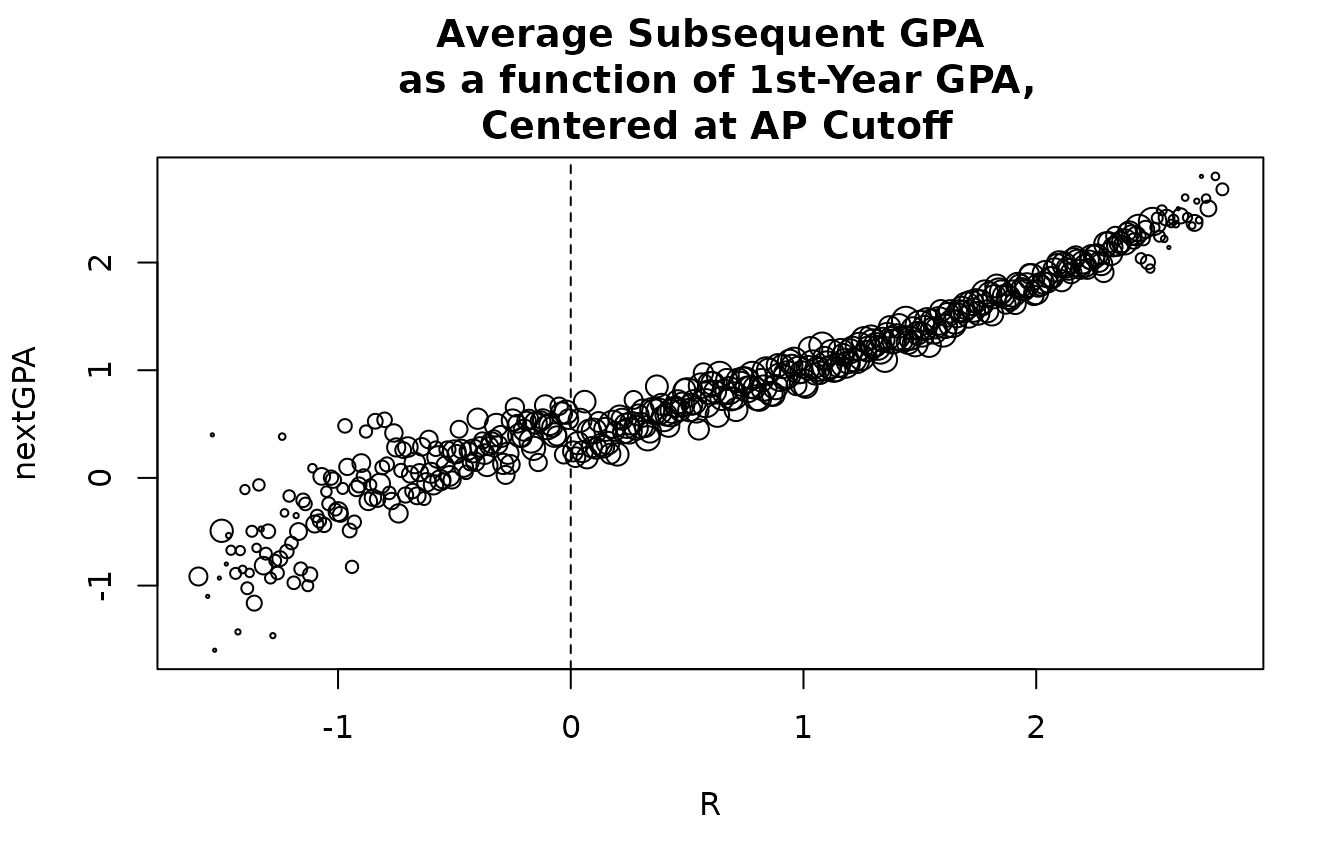

Background

Regression Discontinuity Designs

What characterizes discontinuity (RD) designs, including the LSO study, is that treatment is assigned as a function of a numeric “running variable” $R$, along with a prespecified cutoff value $c$, so that treatment is assigned to subjects $i$ for whom $R_i>c$, or for whom $R_i<c$. If $Z_i$ denote’s $i$’s treatment assignment, we write $Z_i=\mathbf{1}\{R_i<c\}$ or $\mathbf{1}\{R_i<c\}$, where $\mathbf{1}\{x\}$ is the indicator function–equal to 1 when $x$ is true and 0 otherwise. In the LSO study, $i$ indexes students, centered first-year GPA $R_i $ is the running variable, and the treatment under study is AP placement. Then $ Z_i={R_i<0} $. (In “fuzzy” RD designs, $R$’s value relative to $c$ doesn’t completely determine treatment, but merely affects the probability of treatment, so subjects with, say, $R_i>c$ are more likely to be treated than those with $R_i<c$; in fuzzy RD designs, $Z_i=\mathbf{1}\{R_i>c\}$ is typically modeled as an instrument for treatment receipt.)

RD designs hold a privileged place in causal inference, because unlike most other observational study designs, the mechanism for treatment assignment is known. That is, $R$ is the only confounder. On the other hand, since $Z$ is completely determined by $R$, there are no subjects with the same values for $R$ but different values for $Z$, so common observational study techniques, such as matching on $R$, are impossible. Instead, it is necessary to adjust for $R$ with modeling–typically regression.

Analyzing RD Designs with ANCOVA

Traditionally, the typical way to analyze data from RD designs is with ANCOVA, by fitting a regression model such as $$Y_i=\beta_0+\beta_1R_i+\beta_2Z_i+\epsilon_i$$ where $Y_i$ is the outcome of interest measured for subject $i$ (in our example nextGPA), and $\epsilon_i$ is a random regression error. Then, the regression coefficient for $Z$, $\beta_2$, is taken as an estimate of the treatment effect. Common methodological updates to the ANCOVA approach include an interaction term between $Z_i$ and $R_i$, and the substitution semi-parametric regression, such as local linear or polynomial models, for linear ordinary least squares.

Under suitable conditions, the ANCOVA model is said to estimate a “Local Average Treatment Effect” (LATE). If $Y_1$ and $Y_0$ are the potential outcomes for $Y$, then the LATE is defined as $$\displaystyle\lim_{r\rightarrow c^+} E(Y_1|R=r)-\displaystyle\lim_{r\rightarrow c^-} E(Y_0|R=r)$$ or equivalently $$\displaystyle\lim_{\Delta\rightarrow 0^+} E(Y_1-Y_0 |R\in (c-\Delta,c+\Delta))$$ where $E$ denotes expectation–that is, the LATE is the limit of average treatment effects for subjects with $R$ in ever-shrinking regions around $c$.

Among other considerations, the LATE target suggests that data analysts restrict their attention to subjects with $R$ falling within a bandwidth $b>0$ of $c$, e.g. only fitting the model to subjects $i$ with within a “window of analysis” $\mathcal{W}=\{i:R_i\in (c-b,c+b)\}$. A number of methods have been proposed to select $b$, including cross validation, non-parametric modeling of the second derivative of $f(r)=E(Y|R=r)$, and specification tests.

The propertee Approach to RD Designs

The propertee approach to RD designs breaks the data analysis into three steps:

1. Conduct specification tests and choose a bandwidth $b>0$, along with, possibly, other data exclusions, resulting in an analysis sample $W$.
2. Fit a covariance model $Y_{i0}=g(R_i,x_i;\beta)$, modeling $Y_{i0}$ as a function of running variable $R_i$ and (optionally) other covariates $\mathbf{x}_i$. Fitting a covariance model to only the control subjects, as in other designs, would entail extrapolation of a model fit to subjects with $R_i\in (c-b,c)$ to subjects with $R_i\in (c,c+b)$, or vice-versa, which is undesirable. Instead, we fit the covariance model to the full analysis sample $\mathcal{W}$, including both treated and untreated subjects. However, since we are interested in modeling $Y_0$, and not $Y_1$ or $Y$, so rather than fitting $g(\cdot)$, we fit an extended model $$\tilde{g}(R_i,x_i,Z_i;\beta,\gamma)=g(R_i,x_i;\beta)+\gamma Z_i$$ including a term for treatment assignment. The estimate for $\gamma$ is, in essence, a provisional estimate of the treatment effect.
3. Let $\widehat{Y}_{i0}=g(R_i,x_i;\hat{\beta})$, using only the model for $Y_0$—not including the term for $Z$—along with $\hat{\beta}$ estimated in step 2. Then estimate the average treatment effect for subjects in $W$ using the difference in means estimator: $$d_{\hat{\beta}}=\frac{\sum_{i\in W} Z_i(Y_i-\widehat{Y}_{i0})}{\sum_{i \in W} Z_i}-\frac{\sum_{i\in W} (1-Z_i)(Y_i-\widehat{Y}_{i0})}{\sum_{i \in W} (1-Z_i)}$$

The estimator $d_{\hat{\beta}}$ will be consistent if the model $g(R_i,x_i;\beta_0)$, with $\beta_0$ as the probability limit for $\hat{\beta}$, successfully removes all confounding due to $R$, i.e. $Y_0-g(R_i,x_i;\beta_0) \perp \!\!\! \perp Z$ for $i\in \mathcal{W}$.

Analyzing an RD design in propertee

Determining the window of analysis

There is an extensive literature on determining the appropriate window of analysis for an RD design. See, for instance, Imbens and Kalyanaraman (2012) and Sales and Hansen (2020). This stage of the analysis is beyond the scope of this vignette, and does not require the propertee package. For the purpose of this example, we will focus our analysis on $\mathcal{W}=\{i:R_i\in [-0.5,0.5]\}$.

Initializing the RD Design Object

In general, propertee design objects require users to specify a unit of assignment variable, that corresponds to the level of treatment assignment–in other words, which units were assigned between conditions. This is necessary both for combining results across different models or datasets, and for estimating correct design-based standard errors. In lsoSynth, there are no clusters, and individual students are assigned to academic probation on an individual basis. The dataset does not include an ID variable, but any variable that takes a unique value for each row will do. We will use row-names.

lsoSynth$id <- rownames(lsoSynth)

Defining an RD design requires, at minimum, identifying the running variable(s) $R$, as well as how $R$ determines treatment assignment. In our example,

lsoSynth$Z <- lsoSynth$R<0

lsoSynthW <- subset(lsoSynth,abs(R)<=0.5)

#lsoSynthW$id <- 1:nrow(lsoSynthW)
des <- rd_design(Z ~ forcing(R) + unitid(id), data=lsoSynth, subset=abs(lsoSynth$R) <= 0.5)

Modeling $Y_C$ as a function of $R$

We will consider two potential models $\tilde{g}(\cdot)$ of $Y_C$ as a function of $R$. First, the standard OLS model:

### this doesn't work:
g1 <- lm(nextGPA ~ R + Z, data = lsoSynth, weights = ett(des)

##this works, but it's annoying to enter in the subset expression a 2nd time:
g1 <- lm(nextGPA ~ R + Z, data = lsoSynth, subset = abs(R) <= 0.5)

The second is a bounded-influence polynomial model of the type recommended in Sales & Hansen (2020):

g2 <-
if(requireNamespace("robustbase", quietly = TRUE)){
  robustbase::lmrob(nextGPA~poly(R,5)+Z,data=lsoSynthW)
} else g1

[Put something here evaluating them?]

Estimating Effects

yhat1 <- predict(g1,data.frame(R=forcings(des)[[1]],Z=FALSE))
yhat2 <- predict(g2,data.frame(R=forcings(des)[[1]],Z=FALSE))

plot(yhat1,yhat2)

### method 1:

mean(lsoSynthW$nextGPA[lsoSynthW$Z]-yhat1[lsoSynthW$Z])-
  mean(lsoSynthW$nextGPA[!lsoSynthW$Z]-yhat1[!lsoSynthW$Z])
#> [1] 0.2553202

#### method 2:
coef(lm(nextGPA~Z, offset=yhat1,data=lsoSynthW))['ZTRUE']
#>     ZTRUE 
#> 0.2553202

### method 1:

mean(lsoSynthW$nextGPA[lsoSynthW$Z]-yhat2[lsoSynthW$Z])-
  mean(lsoSynthW$nextGPA[!lsoSynthW$Z]-yhat2[!lsoSynthW$Z])
#> [1] 0.2295554

#### method 2:
coef(lm(nextGPA~Z, offset=yhat2,data=lsoSynthW))['ZTRUE']
#>     ZTRUE 
#> 0.2295554